XIAOSUO 记录个人学习的足迹

一、用邻接矩阵表示图

　　邻接矩阵(Adjacentcy Matrix)是用两个数组来表示图，一个数组是一维数组，存储图中的顶点信息，一个数组是二维数组，即矩阵，存储顶点之间相邻的信息，也就是边（或弧）的信息。如果图中有n个顶点，你需要大小为n×n的二维数组来表示图。如下图所示
　　　　
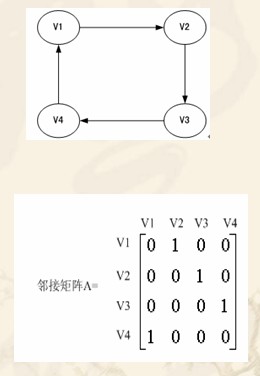　　对邻接矩阵进行操作的代码如下：

public class Node<T>
{
	private T data; //数据域
	//构造器
	public Node(T v)
	{
		data = v;
	}
	//数据域属性
	public T Data
	{
		get
		{
			return data;
		}
		set
		{
			data = value;
		}
	}
}

public class GraphAdjMatrix<T> 
{
	private Node<T>[] nodes; //顶点数组
	private int[,] matrix; //邻接矩阵数组
	private int numEdges; //边的数目
	//初始化邻接矩阵
	public GraphAdjMatrix(int n)
	{
		nodes = new Node<T>[n];
		matrix = new int[n, n];
	}
	//设置索引为index的顶点的信息
	public void SetNode(int index, Node<T> v)
	{
		nodes[index] = v;
	}
	//获取索引为index的顶点的信息
	public Node<T> GetNode(int index)
	{
		return nodes[index];
	}

	//在顶点v1和v2之间添加权值为v的边
	public void SetEdge(Node<T> v1, Node<T> v2, int v)
	{
		//v1或v2不是图的顶点
		if (!IsNode(v1) || !IsNode(v2))
		{
			Console.WriteLine("Node is not belong to Graph!");
			return;
		}

		//矩阵是对称矩阵
		matrix[GetIndex(v1), GetIndex(v2)] = v;
		matrix[GetIndex(v2), GetIndex(v1)] = v;
		++numEdges;
		//为计算最短路径新加的代码,用来将没有边的权值设为无穷大
		for (int i = 0; i < GetNumOfVertex(); i++)
			for (int j = i + 1; j < GetNumOfVertex(); j++)
				if (matrix[i, j] == 0)
				{
					matrix[i, j] = int.MaxValue;
					matrix[j, i] = int.MaxValue;
				}
	}
	//按给定的索引号设置两个顶点之间边
	public void SetEdge(int index1, int index2)
	{
		matrix[index1, index2] = 1;
	}
	//按给定的顶点设置两个顶点之间边
	public void SetEdge(Node<T> v1, Node<T> v2)
	{
		SetEdge(v1, v2, 1);
	}
	//删除顶点v1和v2之间的边
	public void DelEdge(Node<T> v1, Node<T> v2)
	{
		//v1或v2不是图的顶点
		if (!IsNode(v1) || !IsNode(v2))
		{
			Console.WriteLine("Node is not belong to Graph!");
			return;
		}
		//顶点v1与v2之间存在边
		if (matrix[GetIndex(v1), GetIndex(v2)] == 1)
		{
			//矩阵是对称矩阵
			matrix[GetIndex(v1), GetIndex(v2)] = 0;
			matrix[GetIndex(v2), GetIndex(v1)] = 0;
			--numEdges;
		}
	}
	//获取给定的两个索引号所对应的项点之间的边
	public int GetEdge(int index1, int index2)
	{
		return matrix[index1, index2];
	}
	//获取给定的两个顶点之间边
	public int GetEdge(Node<T> v1, Node<T> v2)
	{
		//v1或v2不是图的顶点
		if (!IsNode(v1) || !IsNode(v2))
		{
			Console.WriteLine("Node is not belong to Graph!");
			return 0;
		}
		return matrix[GetIndex(v1), GetIndex(v2)];
	}
	//获取顶点的数目
	public int GetNumOfVertex()
	{
		return nodes.Length;
	}
	//获取边的数目
	public int GetNumOfEdge()
	{
		return numEdges;
	}
	//获取顶点v在顶点数组中的索引
	public int GetIndex(Node<T> v)
	{
		int i = -1;
		//遍历顶点数组
		for (i = 0; i < nodes.Length; ++i)
		{
			//如果顶点v与nodes[i]相等，则v是图的顶点，返回索引值i。
			if (nodes[i].Data.Equals(v.Data))
			{
				return i;
			}
		}
		return i;
	}
	//判断顶点v1与v2之间是否存在边
	public bool IsEdge(Node<T> v1, Node<T> v2)
	{
		//v1或v2不是图的顶点
		if (!IsNode(v1) || !IsNode(v2))
		{
			Console.WriteLine("Node is not belong to Graph!");
			return false;
		}
		//顶点v1与v2之间存在边
		if (matrix[GetIndex(v1), GetIndex(v2)] == 1)
		{
			return true;
		}
		else //不存在边
		{
			return false;
		}
	}
	//判断v是否是图的顶点
	public bool IsNode(Node<T> v)
	{
		//遍历顶点数组
		foreach (Node<T> nd in nodes)
		{
			//如果顶点nd与v相等，则v是图的顶点，返回true
			if (v.Equals(nd))
			{
				return true;
			}
		}
		return false;
	}
}

　　其中用泛型类Node表示图的结点，泛型类GraphAdjMatrix表示邻接矩阵。邻接矩阵中，一维数组nodes用来表示与顶点有关的信息，二维数组matrix用来表示图中的边或弧。

二、用邻接表表示图

　　邻接表的存储方法是一种顺序存储与链式存储相结合的存储方法，顺序存储部分用来保存图中顶点的信息，链式存储部分用来保存图中边（或弧）的信息。具体的做法是：使用一个一维数组，其中每个数组元素包含两个域，其结构如下图所示。
　　　　　　　　

　　　　其中：
　　　　　　顶点域（data）：存放与顶点有关的信息。
　　　　　　头指针域（firstadj）：存放与该顶点相邻接的所有顶点组成的单链表的头指针。

　　邻接单链表中每个结点表示依附于该顶点的一条边，称作边结点，边结点的结构如下图所示。
　 　　　　
　　　　其中：
　　　　　　邻接点域(adjvex)：指示与顶点邻接点在图中的位置，对应着一维数组中的序号，对于有向图，存放的是该边结点所表示的弧的弧头顶点在一维数组中的序号。
　　　　　　数据域(info)：存储边或弧相关的信息，如权值等，当图中边（或弧）不含有信息时，该域可以省略。
　　　　　　链域(nextadj)：指向依附于该顶点的下一个边结点的指针。

　　邻接表表示图列举：

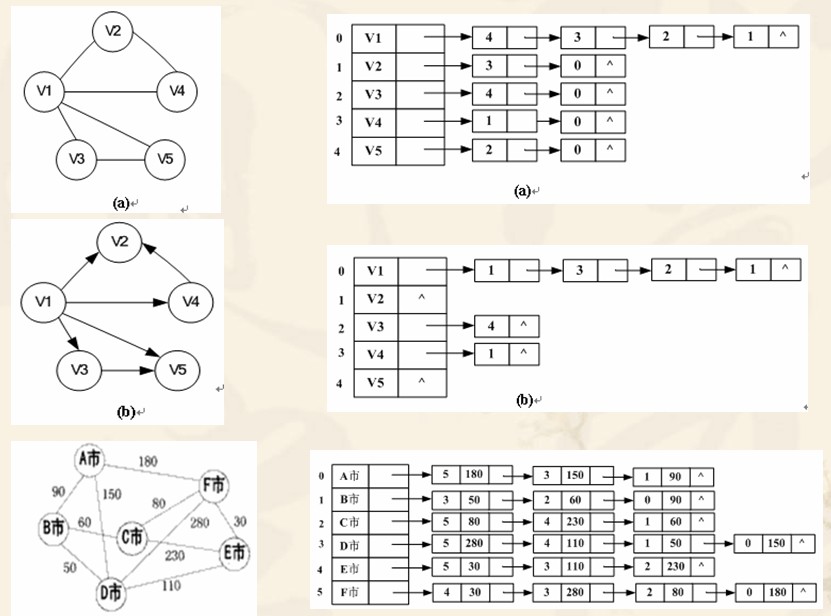　　下面以无向图临接表类的实现来说明图的邻接表类的实现。无向图邻接表的邻接表结点类adjListNode有三个成员字段：一个是adjvex，存储邻接顶点的信息，类型为整型；一个是info，存储边的权值，类型为整型；一个是nextadj，存储下一个邻接表结点的地址，类型为adjListNode。adjListNode类的实现如下所示：

public class adjListNode<T>
{
	private int adjvex; //邻接顶点序号
	private int info;//存储边或弧相关的信息，如权值
	private adjListNode<T> nextadj; //下一个邻接表结点
	//邻接顶点属性
	public int Adjvex
	{
		get
		{ return adjvex; }
		set
		{ adjvex = value; }
	}
	//权值属性
	public int Info
	{
		get
		{ return info; }
		set
		{ info = value; }
	}
	//下一个邻接表结点属性
	public adjListNode<T> NextAdj
	{
		get
		{ return nextadj; }
		set
		{ nextadj = value; }
	}
	//初始化邻接链表
	public adjListNode(int adjvex)
	{
		this.adjvex = adjvex;
		nextadj = null;
	}
	//初始化邻接链表
	public adjListNode(int adjvex, int info)
	{
		this.adjvex = adjvex;
		this.info = info;
		nextadj = null;
	}
}

　　无向图邻接表的顶点结点类VexNode有两个成员字段，一个data，它存储图的等点本身的信息，类型为Node；一个是firstadj，存储顶点的邻接表的第一个结点的地址，类型是adjListNode。VexNode类的实现如下所示：

public class VexNode<T>
{
	private Node<T> data; //图的顶点
	private adjListNode<T> firstadj; //邻接表的第1个结点
	//图的顶点属性
	public Node<T> Data
	{
		get
		{ return data; }
		set
		{ data = value; }
	}
	//邻接表的第1个结点属性
	public adjListNode<T> FirstAdj
	{
		get
		{ return firstadj; }
		set
		{ firstadj = value; }
	}
	//初始化顶点结构
	public VexNode(Node<T> nd)
	{
		data = nd;
		firstadj = null;
	}
	//初始化顶点结构
	public VexNode(Node<T> nd, adjListNode<T> alNode)
	{
		data = nd;
		firstadj = alNode;
	}
}

　　无向图邻接表类GraphAdjList有一个成员字段adjList，表示邻接表数组，数组元素的类型是VexNode。GraphAdjList类操作的实现如下：

public class GraphAdjList<T> 
{
	private VexNode<T>[] adjList;//邻接表数组
	private bool[] visited;//顶点是否被访问过
	//初始化邻接表
	public GraphAdjList(Node<T>[] nodes)
	{
		adjList = new VexNode<T>[nodes.Length];
		for (int i = 0; i < nodes.Length; i++)
		{
			adjList[i] = new VexNode<T>(nodes[i]);
		}
		//以下为添加的代码,用于保存顶点是否被访问过的信息
		visited = new bool[adjList.Length];
		for (int i = 0; i < visited.Length; ++i)
		{
			visited[i] = false;
		}
	}

	//设置索引为index的顶点的信息
	public void SetNode(int index, Node<T> v)
	{
		adjList[index] = new VexNode<T>(v);
	}
	//获取索引为index的顶点的信息
	public Node<T> GetNode(int index)
	{
		return adjList[index].Data;
	}
	//在顶点v1和v2之间添加权值为v的边
	public void SetEdge(Node<T> v1, Node<T> v2, int v)
	{
		//v1或v2不是图的顶点
		if (!IsNode(v1) || !IsNode(v2))
		{
			Console.WriteLine("Node is not belong to Graph!");
			return;
		}
		if (v == 0) return;
		//处理顶点v1的邻接表
		adjListNode<T> p = new adjListNode<T>(GetIndex(v2), v);
		//顶点v1没有邻接顶点
		if (adjList[GetIndex(v1)].FirstAdj == null)
		{
			adjList[GetIndex(v1)].FirstAdj = p;
		}
		//顶点v1有邻接顶点
		else
		{
			p.NextAdj = adjList[GetIndex(v1)].FirstAdj;
			adjList[GetIndex(v1)].FirstAdj = p;
		}
		//处理顶点v2的邻接表
		p = new adjListNode<T>(GetIndex(v1), v);
		//顶点v2没有邻接顶点
		if (adjList[GetIndex(v2)].FirstAdj == null)
		{
			adjList[GetIndex(v2)].FirstAdj = p;
		}
		//顶点v1有邻接顶点
		else
		{
			p.NextAdj = adjList[GetIndex(v2)].FirstAdj;
			adjList[GetIndex(v2)].FirstAdj = p;
		}
	}
	//按给定的索引号设置两个顶点之间边
	public void SetEdge(int index1, int index2)
	{
		SetEdge(GetNode(index1), GetNode(index2), 1);
	}
	//按给定的顶点设置两个顶点之间边
	public void SetEdge(Node<T> v1, Node<T> v2)
	{
		SetEdge(v1, v2, 1);
	}

	//删除顶点v1和v2之间的边
	public void DelEdge(Node<T> v1, Node<T> v2)
	{
		//v1或v2不是图的顶点
		if (!IsNode(v1) || !IsNode(v2))
		{
			Console.WriteLine("Node is not belong to Graph!");
			return;
		}
		//顶点v1与v2之间有边
		if (IsEdge(v1, v2))
		{
			//处理顶点v1的邻接表中的顶点v2的邻接表结点
			adjListNode<T> p = adjList[GetIndex(v1)].FirstAdj;
			adjListNode<T> pre = null;
			while (p != null)
			{
				if (p.Adjvex != GetIndex(v2))
				{
					pre = p;
					p = p.NextAdj;
				}
			}
			pre.NextAdj = p.NextAdj;
			//处理顶点v2的邻接表中的顶点v1的邻接表结点
			p = adjList[GetIndex(v2)].FirstAdj;
			pre = null;
			while (p != null)
			{
				if (p.Adjvex != GetIndex(v1))
				{
					pre = p;
					p = p.NextAdj;
				}
			}
			pre.NextAdj = p.NextAdj;
		}
	}
	//获取给定的两个索引号所对应的项点之间的边
	public int GetEdge(int index1, int index2)
	{
		//v1或v2不是图的顶点
		if (!IsNode(this.GetNode(index1)) || !IsNode(this.GetNode(index2)))
		{
			Console.WriteLine("Node is not belong to Graph!");
			return 0;
		}
		adjListNode<T> p = adjList[index1].FirstAdj;
		while (p != null)
		{
			if (p.Adjvex == index2)
			{
				return p.Info;
			}
			p = p.NextAdj;
		}
		return 0;
	}
	//获取给定的两个顶点之间边的值
	public int GetEdge(Node<T> v1, Node<T> v2)
	{
		//v1或v2不是图的顶点
		if (!IsNode(v1) || !IsNode(v2))
		{
			Console.WriteLine("Node is not belong to Graph!");
			return 0;
		}
		adjListNode<T> p = adjList[GetIndex(v1)].FirstAdj;
		while (p != null)
		{
			if (p.Adjvex == GetIndex(v2))
			{
				return p.Info;
			}
			p = p.NextAdj;
		}
		return 0;
	}
	//获取顶点的数目
	public int GetNumOfVertex()
	{
		return adjList.Length;
	}
	//获取边的数目
	public int GetNumOfEdge()
	{
		int i = 0;
		//遍历邻接表数组
		foreach (VexNode<T> nd in adjList)
		{
			adjListNode<T> p = nd.FirstAdj;
			while (p != null)
			{
				i++;
				p = p.NextAdj;
			}
		}
		return i / 2;
	}
	//获取顶点v在邻接表数组中的索引
	public int GetIndex(Node<T> v)
	{
		int i = -1;
		//遍历邻接表数组
		for (i = 0; i < adjList.Length; ++i)
		{
			//邻接表数组第i项的data值等于v，则顶点v的索引为i
			if (adjList[i].Data.Data.Equals(v.Data))
			{
				return i;
			}
		}
		return i;
	}
	//判断v1和v2之间是否存在边
	public bool IsEdge(Node<T> v1, Node<T> v2)
	{
		//v1或v2不是图的顶点
		if (!IsNode(v1) || !IsNode(v2))
		{
			Console.WriteLine("Node is not belong to Graph!");
			return false;
		}
		adjListNode<T> p = adjList[GetIndex(v1)].FirstAdj;
		while (p != null)
		{
			if (p.Adjvex == GetIndex(v2))
			{
				return true;
			}
			p = p.NextAdj;
		}
		return false;
	}
	//判断v是否是图的顶点
	public bool IsNode(Node<T> v)
	{
		//遍历邻接表数组
		foreach (VexNode<T> nd in adjList)
		{
			//如果v等于nd的data，则v是图中的顶点，返回true
			if (v.Equals(nd.Data))
			{
				return true;
			}
		}
		return false;
	}
 }