Spiga

图（四）：单源最短路径

2012-10-17 17:30:14

　　单源最短路径问题：已知有向带权图(简称有向网)G=(V，E)，找出从某个源点s∈V到V中其余各顶点的最短路径。
一、Dijkstra算法的引入

　　由Dijkstra提出的一种按路径长度递增序产生各顶点最短路径的算法，其算法的基本思想是：设置两个顶点集合T和S，集合S中存放己经找到最短路径的顶点，集合T中存放当前还未找到最短路径的顶点。初始状态时，集合S中只包含源点v0，然后不断从集合T中选取到源点v0路径长度最短的顶点w加入集合S，集合S中每加入一个新的顶点w，都要修改顶点v0到集合T中剩余顶点的最短路径长度值，集合T中各顶点新的最短路径长度值为原来最短路径长度值与顶点w的最短路径长度加上w到该顶点的路径长度值中的较小值。此过程不断重复，直到集合T的顶点全部加入集合S为止。
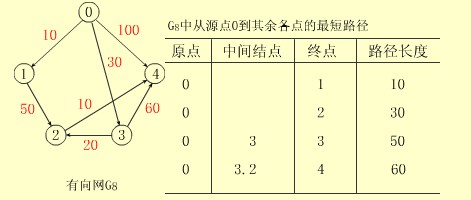
　　【例】在有向网G8中，假定以顶点0为源点，则它则其余各顶点的最短路径按路径递增序排列如下表所示
**　　　　**

二、算法的具体描述

设S为最短距离已确定的顶点集（看作红点集），V-S是最短距离尚未确定的顶点集（看作蓝点集）。

①初始化
　初始化时，只有源点s的最短距离是已知的(SD(s)=0)，故红点集S={s}，蓝点集为空。
**②重复以下工作，按路径长度递增次序产生各顶点最短路径**
　在当前蓝点集中选择一个最短距离最小的蓝点来扩充红点集，以保证算法按路径长度递增的次序产生各顶点的最短路径。
　当蓝点集中仅剩下最短距离为∞的蓝点，或者所有蓝点已扩充到红点集时，s到所有顶点的最短路径就求出来了。
注意：
　①若从源点到蓝点的路径不存在，则可假设该蓝点的最短路径是一条长度为无穷大的虚拟路径。
　②从源点s到终点v的最短路径简称为v的最短路径；s到v的最短路径长度简称为v的最短距离，并记为SD(v)。
在蓝点集中选择一个最短距离最小的蓝点k来扩充红点集
　根据按长度递增序产生最短路径的思想，当前最短距离最小的蓝点k的最短路径是：
　源点，红点1，红点2，…，红点n，蓝点k
距离为：源点到红点n最短距离+<红点n,蓝点k>边长
　为求解方便，设置一个向量D[0．．n-1]，对于每个蓝点v∈ V-S，用D[v]记录从源点s到达v且除v外中间不经过任何蓝点(若有中间点，则必为红点)的"最短"路径长度（简称估计距离）。
　若k是蓝点集中估计距离最小的顶点，则k的估计距离就是最短距离，即若D[k]=min{D[i] i∈V-S}，则D[k]=SD(k)。
　初始时，每个蓝点v的D[c]值应为权w<s，v>，且从s到v的路径上没有中间点，因为该路径仅含一条边<s，v>。
注意：
　在蓝点集中选择一个最短距离最小的蓝点k来扩充红点集是Dijkstra算法的关键
k扩充红点集s后，蓝点集估计距离的修改
　将k扩充到红点后，剩余蓝点集的估计距离可能由于增加了新红点k而减小，此时必须调整相应蓝点的估计距离。
　对于任意的蓝点j，若k由蓝变红后使D[j]变小，则必定是由于存在一条从s到j且包含新红点k的更短路径：P=<s，…，k，j>。且D[j]减小的新路径P只可能是由于路径<s，…，k>和边<k，j>组成。
　所以，当length(P)=D[k]+w<k，j>小于D[j]时，应该用P的长度来修改D[j]的值。

三、Dijkstra算法的实现

　　在邻接矩阵GraphAdjMatrix的方法SetEdge中将没有边的两个顶点之间的权值设为无穷大，然后添加Dijkstra方法，实现如下：

//实现Dijkstra算法
public void Dijkstra(ref int[] distance, Node<T> n)
{
	int v = 0;
	bool[] final = new bool[nodes.Length];
	//初始化
	for (int i = 0; i < nodes.Length; ++i)
	{
		final[i] = false;
		distance[i] = matrix[GetIndex(n), i];
	}
	// n为源点
	distance[GetIndex(n)] = 0;
	final[GetIndex(n)] = true;
	//处理从源点到其余顶点的最短路径
	for (int i = 0; i < nodes.Length; ++i)
	{
		int min = int.MaxValue;
		//比较从源点到其余顶点的路径长度
		for (int j = 0; j < nodes.Length; ++j)
		{
			//从源点到j顶点的最短路径还没有找到
			if (!final[j])
			{
				//从源点到j顶点的路径长度最小
				if (distance[j] < min)
				{
					v = j;
					min = distance[j];
				}
			}
		}
		//源点到顶点k的路径长度最小
		final[v] = true;
		//更新当前最短路径及距离
		for (int w = 0; w < nodes.Length; w++)
			if (final[w] == false)
			{
				if (matrix[v, w] != int.MaxValue && (min + matrix[v, w] < distance[w]))
					distance[w] = min + matrix[v, w];

			}
	}
}