数组(二):特殊矩阵
2012-05-12 11:01:20一、特殊矩阵的定义
对那些具有相同值元素或零元素在矩阵中分布具有一定规律的矩阵,被称之为特殊矩阵。特殊矩阵通常有:
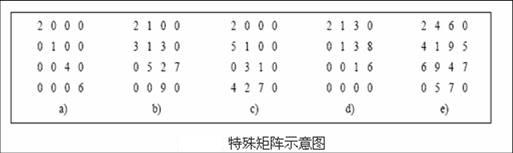
对角矩阵(d i a g o n a l):M是一个对角矩阵当且仅当i≠j 时有M(i, j) = 0。下图a 所示。
三对角矩阵( t r i d i a g o n a l):M是一个三对角矩阵当且仅当| i - j | > 1 时有M(i, j ) = 0。下图b 所示。
下三角矩阵(lower triangular):M是一个下三角矩阵当且仅当i < j 时有M (i, j ) = 0。下图c 所示。
上三角矩阵(upper triangular):M是一个上三角矩阵当且仅当i > j 时有M (i, j ) = 0。下图d 所示。
对称矩阵(s y m m e t r i c):M是一个对称矩阵当且仅当对于所有的i 和j 有M (i, j ) =M (j, i )。下图e 所示。
二、特殊矩阵的压缩存储
由于对称矩阵中的元素关于主对角线对称,为了节省空间,可以为每一对称元素只分配一个存储空间,存储时只存储对称矩阵中的上三角或下三角中的元素 ,这样存储单元的总数是:

可以以行序为主进行压缩存储,也可以以列序为主进行压缩存储。假设以行序为主进行压缩存储,可以用一个一维数组b(n(n+1)/2)作为n阶对称矩阵a的存储结构,则b[k]和矩阵元素aij之间存在如下一对应关系:


