XIAOSUO 记录个人学习的足迹

一、先序遍历（DLR）

　　先序遍历的递归过程为：若二叉树为空，遍历结束。否则，
　　　　（1） 访问根结点；
　　　　（2）先序遍历根结点的左子树；
　　　　（3） 先序遍历根结点的右子树。

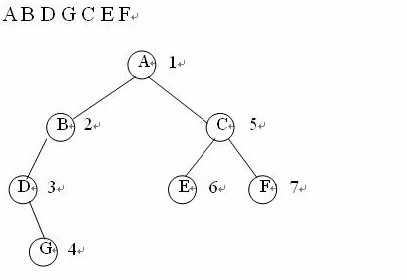
　　算法实现如下：

//前序遍历
public void preorder(Node<T> ptr)
{
	if (IsEmpty())
	{
		Console.WriteLine("Tree is empty");
		return;
	}
	if (ptr != null)
	{
		Console.Write(ptr.Data + "  ");
		preorder(ptr.LChild);
		preorder(ptr.RChild);
	}
}

二、中序遍历（LDR）

　　中序遍历的递归过程为：若二叉树为空，遍历结束。否则，
　　　　（1）中序遍历根结点的左子树；
　　　　（2）访问根结点；
　　　　（3）中序遍历根结点的右子树。

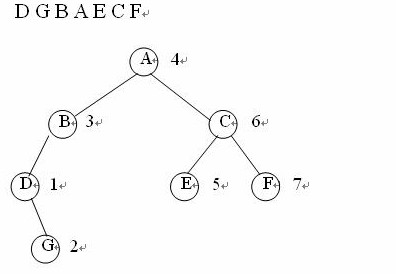
　　算法实现如下：

//中序遍历
public void inorder(Node<T> ptr)
{
	if (IsEmpty())
	{
		Console.WriteLine("Tree is empty");
		return;
	}
	if (ptr != null)
	{
		inorder(ptr.LChild);
		Console.Write(ptr.Data + "  ");
		inorder(ptr.RChild);
	}
}

三、后序遍历（LRD）

　　后序遍历的递归过程为：若二叉树为空，遍历结束。否则，
　　　　（1）后序遍历根结点的左子树；
　　　　（2）后序遍历根结点的右子树。
　　　　（3）访问根结点；

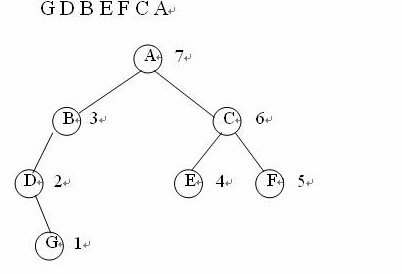
　　算法实现如下：

//后序列遍历
public void postorder(Node<T> ptr)
{
	if (IsEmpty())
	{
		Console.WriteLine("Tree is empty");
		return;
	}
	if (ptr != null)
	{
		postorder(ptr.LChild);
		postorder(ptr.RChild);
		Console.Write(ptr.Data + "  ");
	}
}

四、层次遍历

　　所谓二叉树的层次遍历，是指从二叉树的第一层（根结点）开始，从上至下逐层遍历，在同一层中，则按从左到右的顺序对结点逐个访问。 　　　　　　　　

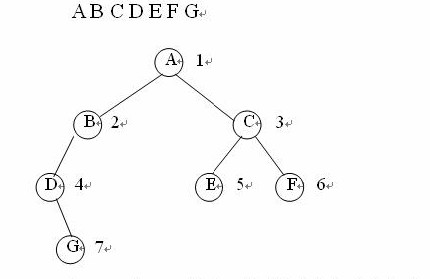
　　算法实现如下：

//层次遍历
public void LevelOrder(Node<T> root)
{
	//根结点为空 
	if (root == null)
	{
		return;
	}

	//设置一个队列保存层序遍历的结点 
	SeqQueue<Node<T>> sq = new SeqQueue<Node<T>>(50);

	//根结点入队 
	sq.EnQueue(root);

	//队列非空，结点没有处理完 
	while (!sq.IsEmpty())
	{
		//结点出队 
		Node<T> tmp = sq.DeQueue();
		//处理当前结点 
		Console.WriteLine("{o}", tmp);

		//将当前结点的左孩子结点入队 
		if (tmp.LChild != null)
		{
			sq.EnQueue(tmp.LChild);
		}
		if (tmp.RChild != null)
		{
			//将当前结点的右孩子结点入队 
			sq.EnQueue(tmp.RChild);
		}
	}
}