树和森林(一):认识树
2012-06-17 18:12:33一、树和森林的定义
树(Tree)是n(n≥0)个结点的有限集T,T为空时称为空树,否则它满足如下两个条件: (1)有且仅有一个特定的称为根(Root)的结点; (2)其余的结点可分为m(m≥0)个互不相交的子集Tl,T2,…,Tm,其中每个子集本身又是一棵树,并称其为根的子树。 森林(Forest)是m(m≥0)棵互不相交的树的集合。 树和森林的概念相近。删去一棵树的根,就得到一个森林;反之,加上一个结点作树根,森林就变为一棵树。
二、树的相关术语
1. 一个结点的子树的个数称为该结点的度。一棵树的度是指该树中结点的最大度数。 2. 树中度为零的结点称为叶结点或终端结点。 3. 树中度不为零的结点称为分枝结点或非终端结点。除根结点外的分枝结点统称为内部结点。 4. 结点的子树的根成为该结点的孩子,相应地,该结点称为孩子的双亲。 5. 如果存在树中的一个结点序列K1,K2,..,Kj,使得结点Ki是结点Ki+1的父结点(1≤i≤j),则称该结点序列是树中从结点K1到结点Kj的一条路径或道路。我们称这条路径的长度为j-1,它是该路径所经过的边(即连接两个结点的线段)的数目。树中任一结点有一条到其自身的长度为零的路径。 6. 如果在树中存在一条从结点K到结点M的路径,则称结点K是结点M的祖先,也称结点M是结点K的子孙或后裔。 7. 我们将树中一个结点的非自身祖先和子孙分别称为该结点的真祖先和真子孙。在一棵树中,树根是唯一没有真祖先的结点。叶结点是那些没有真子孙的结点。子树是树中某一结点及其所有真子孙组成的一棵树。 8. 树中一个结点的高度是指从该结点到作为它的子孙的各叶结点的最长路径的长度。树的高度是指根结点的高度。 9. 从树根到任一结点n有唯一的一条路径,我们称这条路径的长度为结点n的深度或层数。根结点的深度为0,其余结点的深度为其父结点的深度加1。深度相同的结点属于同一层。 10. 树的定义在某些结点之间确定了父子关系,我们又将这种关系延拓为祖先子孙关系。但是树中的许多结点之间仍然没有这种关系。例如兄弟结点之间就没有祖先子孙关系。如果我们在树的每一组兄弟结点之间定义一个从左到右的次序,则得到一棵有序树;否则称为无序树。设结点n的所有儿子按其从左到右的次序排列为n1,n2,..,nk,则我们称n1是n的最左儿子,或简称左儿子,并称ni是ni-1的右邻兄弟,或简称右兄弟(i=2,3,..k)。
三、树的表示
(1)树形图表示
树形图表示是树结构的主要表示方法。树的树形图表示中:结点用圆圈表示,结点的名字写在圆圈旁边(有时亦可写在圆圈内)。
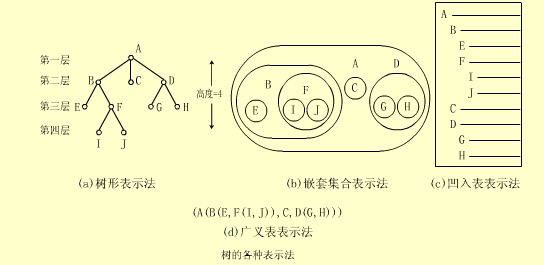
用该定义来分析上图(a)所示的树: 图中的树由结点的有限集T={A,B,C,D,E,F,C,H,I,J}所构成,其中A是根结点,T中其余结点可分成三个互不相交的子集: T1={B,E,F,I,J}, T2=, T3={D,G,H}。 T1、T2和T3是根A的三棵子树,且本身又都是一棵树。例如T1,其根为B,其余结点可分为两个互不相交的的子集T11=和T12={F,I,J},它们都是B的子树。显然T11是只含一个根结点E的树,而T12的根F又有两棵互不相交的子树和,其本身又都是只含一个根结点的树。 (2)嵌套集合表示法 是用集合的包含关系来描述树结构。上图(a)树的嵌套集合表示法如图(b) (3)凹入表表示法 类似于书的目录。上图(a)树的凹入表示法如图(c)
(4)广义表表示法 用广义表的形式表示的。上图(a)树的广义表表示法如图(d)。(A(B(E,F(I,J)),C,D(G,H)))
四、树形结构的逻辑特征 树形结构的逻辑特征可用树中结点之间的父子关系来描述: (1) 树中任一结点都可以有零个或多个直接后继(即孩子)结点,但至多只能有一个直接前趋(即双亲)结点。 (2) 树中只有根结点无前趋,它是开始结点;叶结点无后继,它们是终端结点。 (3) 祖先与子孙的关系是对父子关系的延拓,它定义了树中结点之间的纵向次序。 (4) 有序树中,同一组兄弟结点从左到右有长幼之分。对这一关系加以延拓,规定若k1和k2是兄弟,且k1在k2的左边,则kl的任一子孙都在k2的任一子孙的左边,那么就定义了树中结点之间的横向次序。

