树和森林(二):树的存储结构(上)
2012-06-21 12:58:28一、多重链表表示法
由于树中每个结点都有零个或多个孩子结点,因此,可以令每个结点包括一个结点信息域和多个指针域,每个指针域指向该结点的一个孩子结点,通过各个指针域值反映出树中各结点之间的逻辑关系。这种表示法中,树中每个结点有多个指针域,形成了多条链表,所以这种方法被称为多重链表法。
一个树中各结点的度数各异,因此结点的指针域个数有两种设置方法。方法① 每个结点指针域个数等于该结点的度数;方法② 每个结点指针域个数等于该树的度数。对于方法①它虽然在一定程度上节约了存储空间,但由于树中各个结点的度数是不相同的,各种操作不容易实现,所以一般采用方法②来实现多重链表法。显然,该方法适用于各个结点的度相差不大的情况。 下图为多重链表表示存储结构示意图
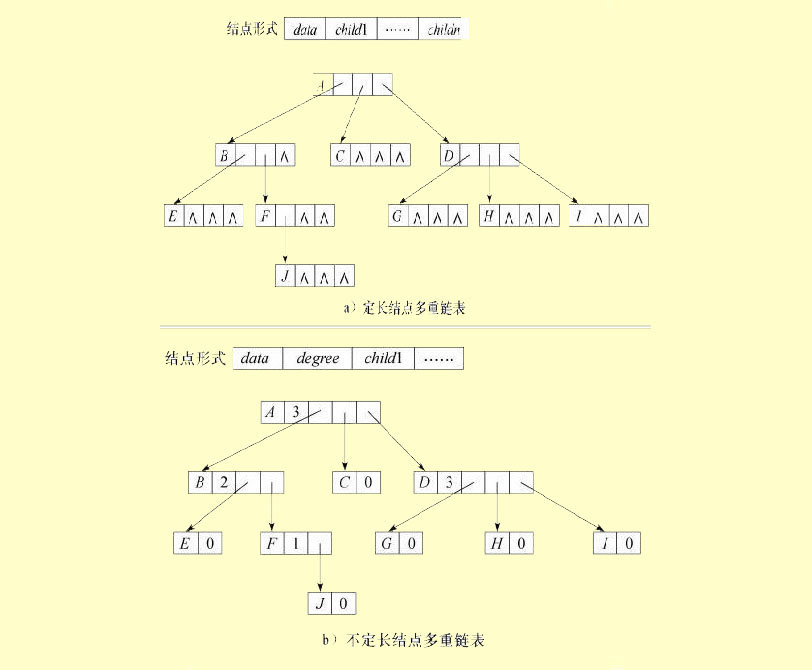
双重链表实现树形结构的代码如下:
public class MLNode<T> {
//存储结点的数据
private T data;
//存储子结点的位置
private MLNode<T>[] childs;
//初始化结点
public MLNode(int max) {
childs = new MLNode<T>[max];
for (int i = 0; i < childs.Length; i++) {
childs[i] = null;
}
}
public T Data
{
get { return data; }
set { data = value; }
}
public MLNode<T>[] Childs{
get { return childs; }
set { childs = value; }
}
}
public class MLTree<T>
{
private MLNode<T> head;
public MLNode<T> Head {
get { return head; }
set { head = value; }
}
public MLTree() {
head = null;
}
public MLTree(MLNode<T> node) {
head = node;
}
//求树的根结点,如果树非空,返回根结点,否则返回空
public MLNode<T> Root()
{
return head;
}
//求结点t的双亲结点。如果t的双亲结点存在,返回双亲结点,否则返回空
public MLNode<T> Parent(MLNode<T> t)
{
MLNode<T> tmp = head;
if (IsEmpty() || t == null) return null;
if (tmp.Data.Equals(t.Data)) return null;
Queue que = new Queue();
que.Enqueue(tmp);
while (que.Count > 0)
{
tmp = (MLNode<T>)que.Dequeue();
for (int i = 0; i < tmp.Childs.Length; i++)
{
if (tmp.Childs[i] != null)
{
if (tmp.Childs[i].Data.Equals(t.Data))
{
return tmp;
}
else
{
que.Enqueue(tmp.Childs[i]);
}
}
}
}
return null;
}
//求结点t的第i个子结点。如果存在,返回第i个子结点,否则返回空
//i=0时表示求第1个子结点
public MLNode<T> Child(MLNode<T> t, int i)
{
if (t!=null && i < t.Childs.Length)
{
return t.Childs[i];
}
else {
return null;
}
}
//求结点t第一个右边兄弟结点。如果存在,返回第一个右边兄弟结点,否则返回空
public MLNode<T> RightSibling(MLNode<T> t)
{
MLNode<T> pn = Parent(t);
if (pn != null)
{
//查找亲兄弟
int i = FindRank(t);
return Child(pn, i + 1);
}
else
{
return null;
}
}
//把以s为头结点的树插入到树中作为结点t的第i棵子树。成功返回true,否则返回false
public bool Insert(MLNode<T> s, MLNode<T> t, int i)
{
if (IsEmpty()) head = t;
t = FindNode(t);
if (t != null && t.Childs.Length > i)
{
t.Childs[i] = s;
return true;
}
else {
return false;
}
}
//删除结点t的第i棵子树。成功返回第i棵子树的根结点,否则返回空
public MLNode<T> Delete(MLNode<T> t, int i)
{
t = FindNode(t);
MLNode<T> node = null;
if (t != null && t.Childs.Length >i) {
node = t.Childs[i];
t.Childs[i] = null;
}
return node;
}
//后序遍历树结点
public void PostOrder(MLNode<T> root) {
if (root == null)
{
return;
}
//按先序访问子树结点
for (int i = 0; i < root.Childs.Length; i++)
{
if (root.Childs[i] != null)
{
PostOrder(root.Childs[i]);
}
}
//访问根结点
Console.Write(root.Data + " ");
}
//先序遍历树结点
public void PreOrder(MLNode<T> root)
{
if (root == null)
{
return;
}
//访问根结点
Console.Write(root.Data + " ");
//按先序访问子树结点
for (int i = 0; i < root.Childs.Length; i++)
{
PreOrder(root.Childs[i]);
}
}
//层序遍历
public void BroadOrder(MLNode<T> root)
{
Console.WriteLine("遍历开始:");
if (root == null)
{
Console.WriteLine("没有结点!");
return;
}
MLNode<T> tmp = root;
Queue que = new Queue();
//根结点入队列
que.Enqueue(tmp);
while (que.Count > 0)
{
//结点出队列并访问
tmp = (MLNode<T>)que.Dequeue();
Console.Write(tmp.Data + " ");
for (int i = 0; i < tmp.Childs.Length; i++)
{
if (tmp.Childs[i] != null)
{
//各个子结点入队列
que.Enqueue(tmp.Childs[i]);
}
}
}
Console.WriteLine("遍历结束.");
}
//按某种方式遍历树
//0:先序
//1:后序
//2:层序
public void Traverse(int TraverseType)
{
if (TraverseType == 0) PreOrder(head);
else if (TraverseType == 1) PostOrder(head);
else BroadOrder(head);
}
//清空树
public void Clear()
{
head = null;
}
//判断树是否为空树。如果是空树,返回true,否则返回false
public bool IsEmpty()
{
return head == null;
}
//求树的深度。如果树不为空,返回树的层次,否则返回0。
public int GetDepth()
{
return 0;
}
//查找结点t在兄弟中的排行,成功时返回位置,否则返回-1
public int FindRank(MLNode<T> t)
{
MLNode<T> pn = Parent(t);
for (int i = 0; i < pn.Childs.Length; i++)
{
MLNode<T> tmp = pn.Childs[i];
if (tmp != null && tmp.Data.Equals(t.Data))
{
return i;
}
}
return -1;
}
//查找在树中的结点t,成功时返回位置,否则返回null
public MLNode<T> FindNode(MLNode<T> t)
{
if (head.Data.Equals(t.Data)) return head;
MLNode<T> pn = Parent(t);
foreach(MLNode<T> tmp in pn.Childs)
{
if (tmp != null && tmp.Data.Equals(t.Data))
{
return tmp;
}
}
return null;
}
public static void TestMLTree() {
MLTree<string> tr = new MLTree<string>();
char ch;
do
{
Console.WriteLine("1. 添加结点");
Console.WriteLine("2. 删除结点");
Console.WriteLine("3. 遍历树");
Console.WriteLine("5. 退出");
Console.WriteLine();
ch = Convert.ToChar(Console.ReadLine());
switch (ch)
{
case '1':
Console.WriteLine("输入父结点:");
string str = Convert.ToString(Console.ReadLine());
MLNode<string> pn = new MLNode<string>(4);
pn.Data = str;
Console.WriteLine("输入子结点:");
str = Convert.ToString(Console.ReadLine());
MLNode<string> cn = new MLNode<string>(4);
cn.Data = str;
Console.WriteLine("输入插入子结点的位置:");
int i = Convert.ToInt32(Console.ReadLine());
bool ok = tr.Insert(cn, pn, i);
if (ok) Console.WriteLine("插入{0}成功",cn.Data);
break;
case '2':
Console.WriteLine("输入要删除的结点:");
str = Convert.ToString(Console.ReadLine());
pn = new MLNode<string>(4);
pn.Data = str;
tr.Delete(pn, 0);
break;
case '3':
tr.Traverse(2);
break;
}
} while (ch != '5');
}
}
**二、双亲表示法
** 双亲表示法利用树中每个结点的双亲唯一性,在存储结点信息的同时,为每个结点附设一个指向其双亲的指针parent,惟一地表示任何-棵树。
下图的双亲表示如下面数组所示。
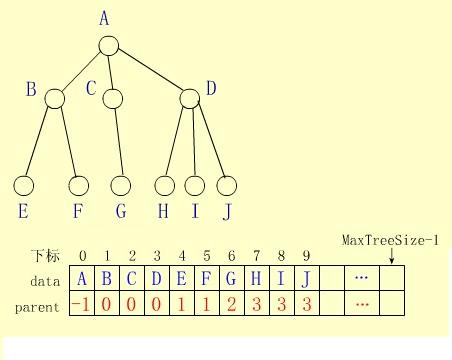 分析:
E和F所在结点的双亲域是1,它们的双亲结点在向量中的位置是1,即B是它们的双亲。
注意:
① 根无双亲,其parent域为-1。
② 双亲表示法中指针parent向上链接,适合求指定结点的双亲或祖先(包括根);求指定结点的孩子或其它后代时,可能要遍历整个数组。
分析:
E和F所在结点的双亲域是1,它们的双亲结点在向量中的位置是1,即B是它们的双亲。
注意:
① 根无双亲,其parent域为-1。
② 双亲表示法中指针parent向上链接,适合求指定结点的双亲或祖先(包括根);求指定结点的孩子或其它后代时,可能要遍历整个数组。
双亲实现树形结构的代码如下:
public class PNode<T>
{
private T data;
private int parent;
public PNode(T val,int pos) {
data = val;
parent = pos;
}
public PNode(PNode<T> node)
{
data = node.data;
parent = node.parent;
}
//结点的数据
public T Data {
get { return data; }
set { data = value; }
}
//指向结点的父结点位置
public int Parent {
get { return parent; }
set { parent = value; }
}
}
public class PTree<T>
{
//用于存储树的结点信息
private PNode<T>[] nodes;
private int maxsize;
private int num; //指示树中已存储的结点数
//构造器
public PTree(int size)
{
nodes = new PNode<T>[size];
maxsize = size;
num = 0;
}
//索引器
public PNode<T> this[int index]
{
get
{
return nodes[index];
}
set
{
nodes[index] = value;
}
}
int Find(PNode<int>[] a,int x){
/*在数组a中查找值为x的元素所属的集合,*/
/*若找到,返回树根结点在数组a中的序号;否则,返回-1*/
int i,j;
i=0;
while (i<a.Length && a[i].Data!=x) i++;
if (i>=a.Length) return -1; /*值为x的元素不属于该组集合,返回-1*/
j=i;
while (a[j].Parent!=-1) j=a[j].Parent;
return j; /*j为该集合的树根结点在数组a中的序号*/
}
//求树的根结点,如果树非空,返回根结点,否则返回空
public PNode<T> Root()
{
if (!IsEmpty())
{
PNode<T> t = Parent(this[0]);
while (t.Parent != -1) {
t = Parent(t);
}
return t;
}
else
{
return null;
}
}
//求结点t的双亲结点。如果t的双亲结点存在,返回双亲结点,否则返回空
public PNode<T> Parent(PNode<T> t)
{
if (t != null && t.Parent != -1)
{
return nodes[t.Parent];
}
else {
return null;
}
}
//求结点t的第1个子结点。如果存在,返回第1个子结点,否则返回空
public PNode<T> Child(PNode<T> t)
{
//查找结点t的存储位置
int pos = FindNode(t);
if (pos != -1)
{
//查找Parent值为pos的结点
for (int k = 0; k < nodes.Length; k++)
{
if (pos == nodes[k].Parent)
{
return nodes[k];
}
}
}
return null;
}
//求结点t的第i个子结点。如果存在,返回第i个子结点,否则返回空
//i=0时表示求第1个子结点
public PNode<T> Child(PNode<T> t, int i)
{
/*
* 在用数组存储的双亲法表示中,
* 假定按树的层次结构从左到右的顺序编号并存储
* 因此第i个子结点为第1个子结点的位置+i
*/
//求t的第1个子结点
PNode<T> cn1 = Child(t);
//查找结点t第一个子结点的存储位置
int pos = FindNode(cn1);
if (pos != -1)
{
//第i个子结点为第一个子结点的位置+i
if (this[pos + i].Parent == cn1.Parent)
return this[pos + i];
}
return null;
}
//求结点t第一个右边兄弟结点。如果存在,返回第一个右边兄弟结点,否则返回空
public PNode<T> RightSibling(PNode<T> t)
{
/*
* 在用数组存储的双亲法表示中,
* 假定按树的层次结构从左到右的顺序编号并存储
* 因此第一个右边兄弟结点的位置即为t结点的位置+1
*/
int pos = FindNode(t);
if (pos != -1)
{
if (nodes[pos + 1].Parent == t.Parent)
{
return nodes[pos + 1];
}
}
return null;
}
//把以s为头结点的树插入到树中作为结点t的第i棵子树。成功返回true,否则返回false
public bool Insert(PNode<T> s,PNode<T> t,int i)
{
//如果为空,则将s作为树的根结点
if (IsEmpty())
{
s.Parent = -1;
nodes[num] = s;
}
else {
PNode<T> cn = Child(t, i);
if (cn != default(PNode<T>))
{
//存在第i个子结点
int pos = FindNode(cn);
MoveBack(pos);
pos = FindNode(t);
if (pos == -1) return false;
s.Parent = FindNode(t);
nodes[pos] = s;
return true;
}
else {
}
}
return true;
}
//删除结点t的第i棵子树。成功返回第i棵子树的根结点,否则返回空
public PNode<T> Delete(PNode<T> t,int i)
{
PNode<T> cn = Child(t, i);
int n = GetNumOfChild(cn);
if (n != 0)
{
for (; n > 0; n--)
{
Delete(cn, n - 1);
}
}
else
{
//是叶子结点
int pos = FindNode(cn);
if (pos != -1)
{
PNode<T> node = new PNode<T>(nodes[pos]);
//删除结点时,将结点后的结点前移一个位置
for (; pos < num; pos++)
{
nodes[pos] = nodes[pos + 1];
}
num--;
return node;
}
}
return null;
}
//按某种方式遍历树
//0:先序
//1:中序
//2:后序
public void Traverse(int TraverseType)
{
}
//清空树
public void Clear()
{
num = 0;
}
//判断树是否为空树。如果是空树,返回true,否则返回false
public bool IsEmpty()
{
return num == 0;
}
//求树的深度。如果树不为空,返回树的层次,否则返回0。
public int GetDepth()
{
return 0;
}
//查找结点t在存储中的位置,成功时返回位置,否则返回-1
public int FindNode(PNode<T> t)
{
if (t != null) //判断结点是否为空
{
for (int i = 0; i < nodes.Length; i++)
{
//结点数据相同且父结点相同
if (this[i].Data.Equals(t.Data) && this[i].Parent == t.Parent)
{
return i;
}
}
}
return -1;
}
//获取结点t的子结点数量
public int GetNumOfChild(PNode<T> t) {
int pos = FindNode(Child(t));
int n=0;
if (pos != -1) {
n=1;
while (nodes[pos].Parent == nodes[++pos].Parent) n++;
}
return n;
}
//前移一个位置
private void MoveForward(int pos) {
for (; pos < num; pos++) {
nodes[pos] = nodes[pos + 1];
}
}
//后移一个位置
private void MoveBack(int pos)
{
for (int i=num; i>pos; i--)
{
nodes[i] = nodes[i-1];
}
}
}

