树和森林(三):树的存储结构(下)
2012-06-23 19:17:06三、 孩子链表表示法
孩子链表表示法是为树中每个结点设置一个孩子链表,并将这些结点及相应的孩子链表的头指针存放在一个向量中。
下面的(a)图就是用孩子链表表示法来存储图中的树。
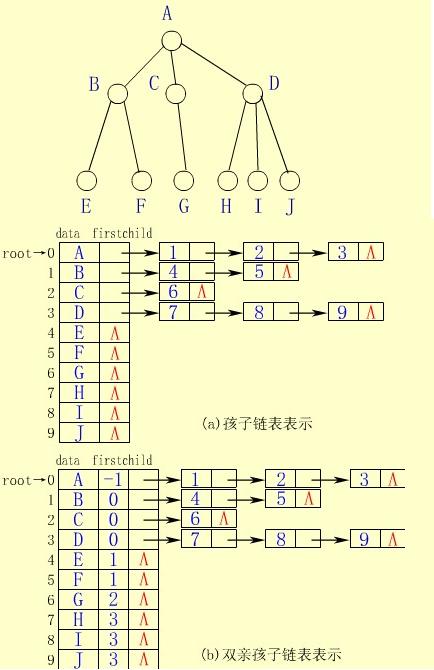
注意: ① 孩子结点的数据域仅存放了它们在向量空间的序号。 ② 与双亲链表表示法相反,孩子链表表示便于实现涉及孩子及其子孙的运算,但不便于实现与双亲有关的运算。 ③ 将双亲链表表示法和孩子链表表示法结合起来,可形成双亲孩子链表表示法。
孩子链表实现树形结构的代码如下:
public class ChildNode
{
private int pos;
private ChildNode nextChild;
public ChildNode() {
pos = -1;
nextChild = null;
}
public ChildNode(int p, ChildNode nc) {
pos = p;
nextChild = nc;
}
//孩子结点在一维数组中的位置序号
public int Pos {
get { return pos; }
set { pos = value; }
}
//下一个孩子结点的地址信息
public ChildNode NextChild {
get { return nextChild; }
set { nextChild = value; }
}
}
public class CLNode<T>
{
private T data;
private ChildNode firstChild;
public CLNode(){
data = default(T);
firstChild = null;
}
public CLNode(T d, ChildNode c)
{
data = d;
firstChild = c;
}
//孩子结点的数据信息
public T Data {
get { return data; }
set { data = value; }
}
//第一个孩子结点的信息
public ChildNode FirstChild {
get { return firstChild; }
set { firstChild = value; }
}
}
public class CLTree<T>
{
private CLNode<T>[] nodes;
public CLTree(int size) {
nodes = new CLNode<T>[size];
for (int i = 0; i < nodes.Length; i++) {
nodes[i].Data = default(T);
nodes[i].FirstChild = null;
}
}
//索引器
public CLNode<T> this[int index]
{
get{return nodes[index];}
set { nodes[index] = value; }
}
//求树的根结点,如果树非空,返回根结点,否则返回空
public CLNode<T> Root()
{
return null;
}
//求结点t的双亲结点。如果t的双亲结点存在,返回双亲结点,否则返回空
public CLNode<T> Parent(CLNode<T> t)
{
return null;
}
//求结点t的第i个子结点。如果存在,返回第i个子结点,否则返回空
//i=0时表示求第1个子结点
public CLNode<T> Child(CLNode<T> t, int i)
{
if (t != null)
{
ChildNode tmp = t.FirstChild;
if(i==0 && tmp != null){
return nodes[tmp.Pos];
}
else
{
int k = 0;
while (tmp !=null && tmp.NextChild != null && k < i)
{
tmp = tmp.NextChild;
k++;
}
if (k == i) return nodes[tmp.Pos];
}
}
return null;
}
//求结点t第一个右边兄弟结点。如果存在,返回第一个右边兄弟结点,否则返回空
public CLNode<T> RightSibling(CLNode<T> t)
{
return null;
}
//把以s为头结点的树插入到树中作为结点t的第i棵子树。成功返回true,否则返回false
public bool Insert(CLNode<T> s, CLNode<T> t, int i)
{
//如果是空树,则将t作为根结点插入;
if (IsEmpty())
{
//存储父结点
int pos1 = FindBlank();
nodes[pos1].Data = t.Data;
//存储子结点
int pos2 = FindBlank();
nodes[pos2].Data = s.Data;
ChildNode cn = new ChildNode(pos2, null);
nodes[pos1].FirstChild = cn;
return true;
}
else {
int pos1 = FindNode(t);
if (pos1 != -1) {
t = nodes[pos1];
int pos2 = FindBlank();
if (pos2 != 0)
{ //检查空间
nodes[pos2].Data = s.Data;
ChildNode cn = new ChildNode(pos2, null);
//修改孩子链表,将新增的结点添加到孩子链表
ChildNode tmp = t.FirstChild;
while (tmp.NextChild != null) tmp = tmp.NextChild;
tmp.NextChild = cn;
return true;
}
}
return false;
}
}
//删除结点t的第i棵子树。成功返回第i棵子树的根结点,否则返回空
public CLNode<T> Delete(CLNode<T> t, int i)
{
int pos = FindNode(t);
if (pos != -1)
{
t.FirstChild = nodes[pos].FirstChild;
nodes[pos].Data = default(T);
return t;
}
else
{
return null;
}
}
//按某种方式遍历树
//0:先序
//1:中序
//2:后序
public void Traverse(int TraverseType)
{
}
//清空树
public void Clear()
{
for (int i = 0; i < nodes.Length; i++) {
nodes[i].Data = default(T);
}
}
//判断树是否为空树。如果是空树,返回true,否则返回false
public bool IsEmpty()
{
int i;
for (i = 0; i < nodes.Length; i++)
{
if (!nodes[i].Data.Equals(default(T))) break;
}
return i>= nodes.Length ;
}
//求树的深度。如果树不为空,返回树的层次,否则返回0。
public int GetDepth()
{
return 0;
}
//寻找一个可用的空间,成功时返回位置,否则返回-1
private int FindBlank() {
for (int i = 0; i < nodes.Length; i++) {
if (nodes[i].Data.Equals(default(T))) return i;
}
return -1;
}
//查找结点成功时,返回结点下标,否则返回-1;
private int FindNode(CLNode<T> t) {
for (int i = 0; i < nodes.Length; i++) {
if(nodes[i].Data.Equals(t.Data)){
return i;
}
}
return -1;
}
public static void TestCLTree()
{
CLTree<string> tr = new CLTree<string>(30);
char ch;
do
{
Console.WriteLine("1. 添加结点");
Console.WriteLine("2. 删除结点");
Console.WriteLine("3. 查找结点");
Console.WriteLine("4. 遍历树");
Console.WriteLine("5. 退出");
Console.WriteLine();
ch = Convert.ToChar(Console.ReadLine());
switch (ch)
{
case '1':
Console.WriteLine("输入父结点:");
string str = Convert.ToString(Console.ReadLine());
CLNode<string> pn = new CLNode<string>();
pn.Data = str;
Console.WriteLine("输入子结点:");
str = Convert.ToString(Console.ReadLine());
CLNode<string> cn = new CLNode<string>();
cn.Data = str;
Console.WriteLine("输入插入子结点的位置:");
int i = Convert.ToInt32(Console.ReadLine());
bool ok = tr.Insert(cn, pn, i);
if (ok) Console.WriteLine("插入{0}成功", cn.Data);
break;
case '2':
Console.WriteLine("输入要删除的结点:");
str = Convert.ToString(Console.ReadLine());
pn = new CLNode<string>();
pn.Data = str;
tr.Delete(pn, 0);
break;
case '3':
break;
case '4':
tr.Traverse(0);
break;
}
} while (ch != '5');
}
}
四、双亲孩子表示法
双亲孩子表示法是将双亲表示法和孩子链表表示法相结合的结果。其仍将各结点的孩子结点分别组成单链表,同时用一维数组顺序存储树中的各结点,数组元素除了包括结点本身的信息和该结点的孩子结点链表的头指针之外,还增加一个域,存储该结点双亲结点在数组中的序号。 在孩子表示法的示意图(b)中就是用双亲孩子表示法来存储图中的树。 双亲孩子表示法的代码实现如下:
public class PCLNode<T>
{
private T data;
private int parent;
private ChildNode firstChild;
public PCLNode(){
data = default(T);
parent = -1;
firstChild = null;
}
public PCLNode(T d, int p,ChildNode c)
{
data = d;
parent = p;
firstChild = c;
}
//孩子结点的数据信息
public T Data {
get { return data; }
set { data = value; }
}
//第一个孩子结点的信息
public ChildNode FirstChild {
get { return firstChild; }
set { firstChild = value; }
}
//父结点的位置
public int Parent {
get { return parent; }
set { parent = value; }
}
}
public class PCLTree<T>
{
private PCLNode<T>[] nodes;
public PCLTree(int size)
{
nodes = new PCLNode<T>[size];
Console.Write(nodes[0]);
}
//索引器
public PCLNode<T> this[int index]
{
get { return nodes[index]; }
set { nodes[index] = value; }
}
//求树的根结点,如果树非空,返回根结点,否则返回空
public PCLNode<T> Root()
{
if (IsEmpty())
{
return null;
}
else
{
return nodes[0];
}
}
//求结点t的双亲结点。如果t的双亲结点存在,返回双亲结点,否则返回空
public PCLNode<T> Parent(PCLNode<T> t)
{
if (t != null && t.Parent != -1)
{
return nodes[t.Parent];
}
else {
return null;
}
}
//求结点t的第i个子结点。如果存在,返回第i个子结点,否则返回空
//i=0时表示求第1个子结点
public PCLNode<T> Child(PCLNode<T> t, int i)
{
int k = FindNode(t);
if (k != -1)
{
ChildNode tmp = t.FirstChild;
if (i == 0) return nodes[tmp.Pos];
k = 0;
//从孩子链表中查找第i个孩子结点
while (tmp.NextChild != null && k < i)
{
tmp = tmp.NextChild;
k++;
}
if (i == k)
{
return nodes[tmp.Pos];
}
}
return null;
}
//求结点t第一个右边兄弟结点。如果存在,返回第一个右边兄弟结点,否则返回空
public PCLNode<T> RightSibling(PCLNode<T> t)
{
return null;
}
//把以s为头结点的树插入到树中作为结点t的第i棵子树。成功返回true,否则返回false
public bool Insert(PCLNode<T> s, PCLNode<T> t, int i)
{
//如果是空树,则将t作为根结点插入;
if (IsEmpty())
{
//存储父结点
int pos1 = FindBlank();
nodes[pos1] = t;
t.Parent = -1;
//存储子结点
int pos2 = FindBlank();
nodes[pos2]=s;
s.Parent = pos1;
ChildNode cn = new ChildNode(pos2, null);
nodes[pos1].FirstChild = cn;
return true;
}
else
{
int pos1 = FindNode(t);
if (pos1 != -1)
{
t = nodes[pos1];
int pos2 = FindBlank();
if (pos2 != 0)
{ //检查空间
nodes[pos2]=s;
s.Parent = pos1;
ChildNode cn = new ChildNode(pos2, null);
//修改孩子链表,将新增的结点添加到孩子链表
ChildNode tmp = t.FirstChild;
if (tmp == null)
{
t.FirstChild = cn;
}
else
{
while (tmp.NextChild != null) tmp = tmp.NextChild;
tmp.NextChild = cn;
}
return true;
}
}
return false;
}
}
//删除结点t的第i棵子树。成功返回第i棵子树的根结点,否则返回空
public PCLNode<T> Delete(PCLNode<T> t, int i)
{
int pos = FindNode(t);
//从孩子结点中删除
ChildNode old=null,tmp = nodes[pos].FirstChild;
while (tmp != null)
{
if (tmp.Pos == pos)
{
old = tmp;
tmp = tmp.NextChild;
break;
}
else
{
tmp = tmp.NextChild;
}
}
if(old != null){
PCLNode<T> cn = nodes[old.Pos];
for (i = NumOfChild(cn) - 1; i >= 0; i--) {
Delete(cn, i);
}
}
if (pos != -1)
{
//从树结点中删除
t.FirstChild = nodes[pos].FirstChild;
t.Parent = nodes[pos].Parent;
nodes[pos]=null;
//从孩子链表中删除
if (t.Parent != -1)
{
tmp = nodes[t.Parent].FirstChild;
while (tmp != null) {
if (tmp.Pos == pos)
{
tmp = tmp.NextChild;
break;
}
else {
tmp = tmp.NextChild;
}
}
}
return t;
}
else
{
return null;
}
}
//按某种方式遍历树
//0:先序
//1:中序
//2:后序
public void Traverse(int TraverseType)
{
for (int i = 0; i < nodes.Length; i++) {
if(nodes[i]!=null){
Console.WriteLine();
Console.Write(nodes[i].Data);
ChildNode tmp = nodes[i].FirstChild;
while(tmp != null){
Console.Write(nodes[tmp.Pos].Data);
tmp = tmp.NextChild;
}
}
}
}
//清空树
public void Clear()
{
for (int i = 0; i < nodes.Length; i++)
{
nodes[i]=null;
}
}
//判断树是否为空树。如果是空树,返回true,否则返回false
public bool IsEmpty()
{
int i;
for (i = 0; i < nodes.Length; i++)
{
if (!(nodes[i]==null)) break;
}
return i >= nodes.Length;
}
//求树的深度。如果树不为空,返回树的层次,否则返回0。
public int GetDepth()
{
return 0;
}
//寻找一个可用的空间,成功时返回位置,否则返回-1
private int FindBlank()
{
for (int i = 0; i < nodes.Length; i++)
{
if (nodes[i]==null) return i;
}
return -1;
}
//查找结点成功时,返回结点下标,否则返回-1;
private int FindNode(PCLNode<T> t)
{
for (int i = 0; i < nodes.Length; i++)
{
if (nodes[i] !=null && nodes[i].Data.Equals(t.Data))
{
t.FirstChild = nodes[i].FirstChild;
t.Parent = nodes[i].Parent;
return i;
}
}
return -1;
}
private int NumOfChild(PCLNode<T> t){
ChildNode cn = t.FirstChild;
int i = 0;
while(cn != null){
i++;
cn = cn.NextChild;
}
return i;
}
public static void TestTree()
{
PCLTree<string> tr = new PCLTree<string>(30);
char ch;
do
{
Console.WriteLine("1. 添加结点");
Console.WriteLine("2. 删除结点");
Console.WriteLine("3. 查找结点");
Console.WriteLine("4. 遍历树");
Console.WriteLine("5. 退出");
Console.WriteLine();
ch = Convert.ToChar(Console.ReadLine());
switch (ch)
{
case '1':
Console.WriteLine("输入父结点:");
string str = Convert.ToString(Console.ReadLine());
PCLNode<string> pn = new PCLNode<string>();
pn.Data = str;
Console.WriteLine("输入子结点:");
str = Convert.ToString(Console.ReadLine());
PCLNode<string> cn = new PCLNode<string>();
cn.Data = str;
Console.WriteLine("输入插入子结点的位置:");
int i = Convert.ToInt32(Console.ReadLine());
bool ok = tr.Insert(cn, pn, i);
if (ok) Console.WriteLine("插入{0}成功", cn.Data);
break;
case '2':
Console.WriteLine("输入要删除的结点:");
str = Convert.ToString(Console.ReadLine());
pn = new PCLNode<string>();
pn.Data = str;
tr.Delete(pn, 0);
break;
case '3':
break;
case '4':
tr.Traverse(0);
break;
}
} while (ch != '5');
}
}
五、孩子兄弟链表表示法 在存储结点信息的同时,附加两个分别指向该结点最左孩子和右邻兄弟的指针域leftmostchild和rightsibling,即可得树的孩子兄弟链表表示。
下面的图就是用孩子兄弟链表表示法来存储图中的树。
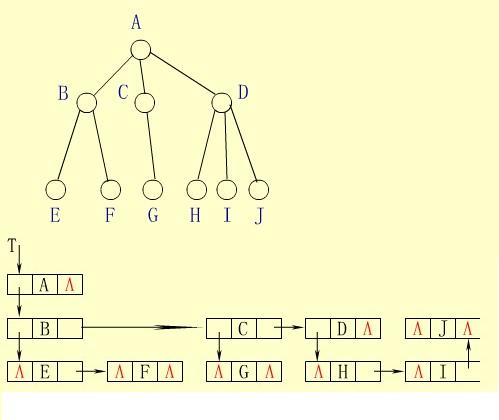 注意:
这种存储结构的最大优点是:它和二叉树的二叉链表表示完全一样。可利用二叉树的算法来实现对树的操作。
注意:
这种存储结构的最大优点是:它和二叉树的二叉链表表示完全一样。可利用二叉树的算法来实现对树的操作。
孩子兄弟表示法的代码结构如下,具体实现请二叉树部分:
public class CSNode<T>
{
private T data;
private CSNode<T> firstChild;
private CSNode<T> nextSibling;
public CSNode() {
data = default(T);
firstChild = null;
nextSibling = null;
}
//结点的数据
public T Data {
get { return data; }
set { data = value; }
}
//结点的第一个孩子
public CSNode<T> FirstChild {
get { return firstChild; }
set { nextSibling = value; }
}
//结点右边的第一个兄弟
public CSNode<T> NextSibling {
get { return nextSibling; }
set { nextSibling = value; }
}
}
public class CSTree<T>
{
CSNode<T> head;
public CSNode<T> Head {
get { return head; }
set { head = value; }
}
//求树的根结点,如果树非空,返回根结点,否则返回空
public CSNode<T> Root()
{
return head;
}
//求结点t的双亲结点。如果t的双亲结点存在,返回双亲结点,否则返回空
public CSNode<T> Parent(CSNode<T> t)
{
return null;
}
//求结点t的第i个子结点。如果存在,返回第i个子结点,否则返回空
//i=0时表示求第1个子结点
public CSNode<T> Child(CSNode<T> t, int i)
{
return null;
}
//求结点t第一个右边兄弟结点。如果存在,返回第一个右边兄弟结点,否则返回空
public CSNode<T> RightSibling(CSNode<T> t)
{
return null;
}
//把以s为头结点的树插入到树中作为结点t的第i棵子树。成功返回true,否则返回false
public bool Insert(CSNode<T> s, CSNode<T> t, int i)
{
return false;
}
//删除结点t的第i棵子树。成功返回第i棵子树的根结点,否则返回空
public CSNode<T> Delete(CSNode<T> t, int i)
{
return null;
}
//按某种方式遍历树
//0:先序
//1:中序
//2:后序
public void Traverse(int TraverseType)
{
}
//清空树
public void Clear()
{
head = null;
}
//判断树是否为空树。如果是空树,返回true,否则返回false
public bool IsEmpty()
{
return head == null;
}
//求树的深度。如果树不为空,返回树的层次,否则返回0。
public int GetDepth()
{
return 0;
}
//寻找一个可用的空间,成功时返回位置,否则返回-1
private int FindBlank()
{
return -1;
}
//查找结点成功时,返回结点下标,否则返回-1;
private int FindNode(CSNode<T> t)
{
return -1;
}
private int NumOfChild(CSNode<T> t)
{
return 0;
}
}

