Spiga

内排序（四）：堆排序

2012-07-14 11:58:01

一、基本思想

　　堆排序是针对直接选择排序所存在的上述问题的一种改进方法。它在寻找当前关键字最小记录的同时，还保存了本次排序过程中所产生的其他比较信息。
　　设有n个元素组成的序列{a0,a1,…an-1}，若满足下面的条件：
（1）这些元素是一棵完全二叉树的结点，且对于i=0，1，…，n-1，ai是该完全二叉 树编号为i的结点；
（2）满足下列不等式：
　　　　　　
　　　　　　则称该序列为一个堆。堆分为最大堆和最小堆两种。满足不等式(a)的为最小堆，满足不等式(b)的为最大堆。
　　

　　
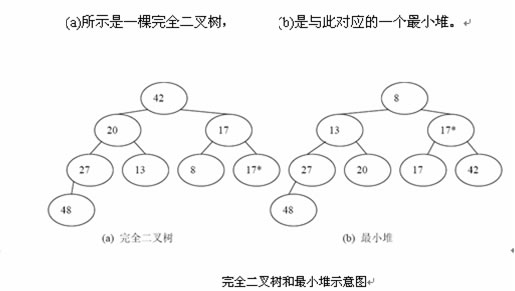
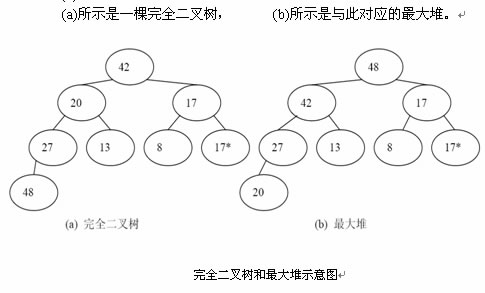　　由堆的定义可知，堆有如下两个性质：
（1）最大堆的根结点是堆中关键码最大的结点，最小堆的根结点是堆中关键码最小的结点，我们称堆的根结点记录为堆顶记录。
（2）对于最大堆，从根结点到每个叶子结点的路径上，结点组成的序列都是递减有序的；对于最小堆，从根结点到每个叶子结点的路径上，结点组成的序列都是递增有序的。
　　将待排序的记录序列建成一个堆，并借助于堆的性质进行排序的方法叫作堆排序。堆排序的基本思想是：设有n个记录，首先将这n个记录按关键码建成堆，将堆顶记录输出，得到n个记录中关键码最大（或最小）的记录；调整剩余的n-1个记录，使之成为一个新堆，再输出堆顶记录；如此反复，当堆中只有一个元素数时，整个序列的排序结束，得到的序列便是原始序列的非递减或非递增序列。
　　从堆排序的基本思想中可看出，在堆排序的过程中，主要包括两方面的工作：
（1）如何将原始的记录序列按关键码建成堆；
（2）输出堆顶记录后，怎样调整剩下记录，使其按关键码成为一个新堆。

　　首先，以最大堆为例讨论第一个问题：如何将n个记录的序列按关键码建成堆。 考虑数字序列70、30、40、10、80、20、91、100、75、60、45
　　　　
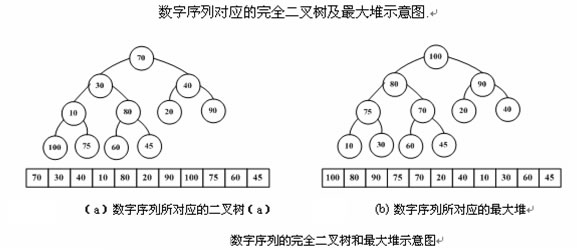　　完全二叉树构建最大堆的示意图
　　　　　　　　

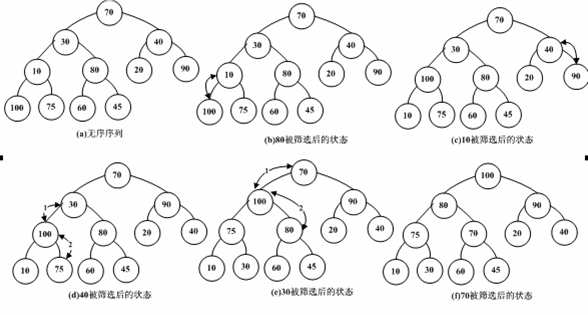
二、堆排序的实现

　　在实现堆排序算法之前，先要实现将完全二叉树构建成最大堆的算法，然后在构建的堆之上实现堆排序，具体实现如下：

public class HeapSort
{
    static int _count;  

    public static List<int> Demo(List<int> data)
    {
        Build(data);

        for (var i = data.Count - 1; i > 0; i--)
        {
            Swap(data, 0, i);
            _count--;
            Heapify(data, 0);
        }
        return data;
    }
    static void Build(List<int> data)
    {   // 建立大顶堆
        _count = data.Count;
        for (var i = (int)Math.Floor(((decimal)(_count / 2))); i >= 0; i--)
        {
            Heapify(data, i);
        }
    }

    static void Heapify(List<int> data, int i)
    {
        int left = 2 * i + 1,
        right = 2 * i + 2,
        largest = i;

        if (left < _count && data[left] > data[largest])
        {
            largest = left;
        }

        if (right < _count && data[right] > data[largest])
        {
            largest = right;
        }

        if (largest != i)
        {
            Swap(data, i, largest);
            Heapify(data, largest);
        }
    }

    static void Swap(List<int> data, int i, int j)
    {
        var temp = data[i];
        data[i] = data[j];
        data[j] = temp;
    }

}

三、时间复杂度分析

　　对深度为k的堆，“筛选”所需进行的关键字比较的次数至多为2(k-1);
对n个关键字，建成深度为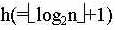的堆，所需进行的关键字比较的次数至多为4n;
　　调整“堆顶”n-1次，总共进行的关键字比较的次数不超过
　　　　

　　　　
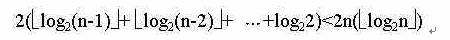　　因此，堆排序的在最坏的情况下，时间复杂度为O(nlog2n)，这是堆的最大优点。堆排序方法在记录较少的情况下并不提倡，但对于记录较多的数据列表还是很有效的。因为其运行时间主要耗费在建初始堆和调整新建堆时的进行的返复筛选上。