Spiga

内排序（一）：插入排序

2012-07-05 16:20:23

插入排序(Insertion Sort)的基本思想是：每次将一个待排序的记录，按其关键字大小插入到前面已经排好序的数据序列的适当位置，直到全部记录插入完成为止。

一、基本思想

　　假设待排序的记录存放在数组R[0…n-1]中。初始时，R[0]自成1个有序区，无序区为R[1…n-1]。从i=1起直至i= n-1为止，依次将R[i]插入当前的有序区R[0…i-1]中，生成含n个记录的有序区。
　　通常将一个记录Ri插入到当前的有序区，使得插入后仍保证该区间里的记录是按关键字有序的操作称第i趟插入排序。
　　排序过程的某一中间时刻，R被划分成两个子区间R[0…i-1]（已排好序的有序区）和[i…n-1]（当前未排序的部分，可称无序区）。
　　插入排序的基本操作是将当前无序区的第1个记录R[0]插人到有序区R[0…i-1]中适当的位置上，使 R[0…i]变为新的有序区。因为这种方法每次使有序区增加1个记录，通常称增量法。
　　下图为插入排序是示意图：
　　　　

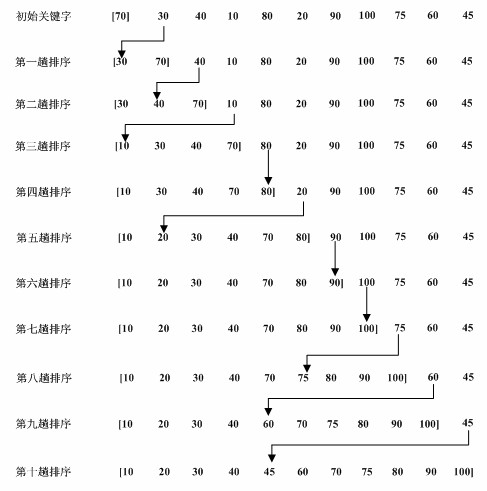
二、插入排序的实现

public class InsertSort
{
    public static List<int> Demo(List<int> data)
    { 
        int preIndex, currentIndex;
        for (var i = 1; i < data.Count; i++)
        {
            preIndex = i - 1;
            currentIndex = data[i];
            while (preIndex >= 0 && data[preIndex] > currentIndex)
            {
                data[preIndex + 1] = data[preIndex];
                preIndex--;
            }
            data[preIndex + 1] = currentIndex;
        }
        return data;
    }
}

三、时间复杂度分析

　　插入排序算法的时间复杂度分为最好、最坏和随机三种情况：
　　　　（1）最好的情况是关键字在序列中顺序有序。这时外层循环的比较次数为n-1，if条件的比较次数为n-1,内层循环的次数为0。这样，外层循环中每次记录的比较次数为2，整个序列的排序所需的记录关键字的比较次数为2(n-1)，移动次数为0，所以插入排序算法在最好情况下的时间复杂度为O(n)。
　　　　（2）最坏情况是关键字在记录序列中逆序有序。这时内层循环的循环系数每次均为i。这样，整个外层循环的比较次数为：
　　　　　　
　　　　　　因此，插入排序算法在最坏情况下的时间复杂度为O(n2)。
　　　　（3）如果顺序表中的记录的排列是随机的，则记录的期望比较次数为n2/4。因此，插入排序算法在一般情况下的时间复杂度为O(n2)。
可以证明，顺序表中的记录越接近于有序，插入排序算法的时间效率越高，其时间效率在O(n)到O(n2)之间。
　　总的说来，插入排序所需进行关键字间的比较次数和记录移动的次数均为n2/4，所以插入排序的时间复杂度为O(n2)。