内排序(六):快速排序
2012-07-26 21:12:12快速排序是C.R.A.Hoare于1962年提出的一种分区交换排序。它采用了一种分治法(Divide-and-ConquerMethod)策略,分治法的基本思想是:将原问题分解为若干个规模更小但结构与原问题相似的子问题。递归地解这些子问题,然后将这些子问题的解组合为原问题的解。快速排序是目前己知的平均速度最快的一种排序方法。
一、基本思想
快速排序方法的基本思想是:从待排序的n个记录中任意选取一个记录Ri(通常选取序列中的第一个记录)作标准,调整序列中各个记录的位置,使排在Ri前面的记录的关键字都小于Ri的关键字,排在Ri后面的记录的关键字都大于Ri的关键字,我们把这样一个过程称作一次快速排序。在第一次快速排序中,确定了所选取的记录Ri最终在序列中的排列位置,同时也把剩余的记录分成了两个子序列。对两个子序列分别进行快速排序,又确定了两个记录在序列中应处的位置,并将剩余的记录分成了四个子序列,如此重复下去,当各个子序列的长度为1时,全部记录排序完毕。
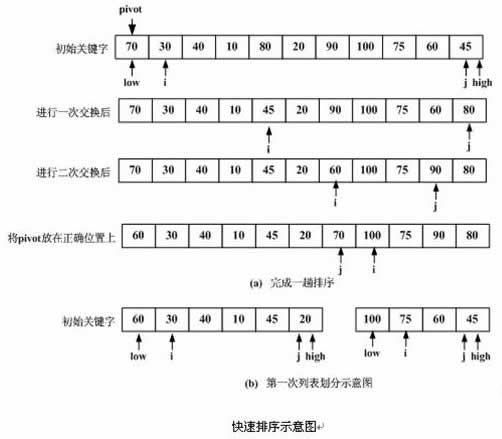
二、快速排序的实现
public class QuickSort
{
//排序算法---> 遍历-->判断 --->交换<-------降低
public static List<int> Demo(List<int> data, int left = 0, int? right = null)
{
int len = data.Count, partitionIndex;
right = right ?? data.Count - 1;
if (left < right)
{
partitionIndex = partition(data, left, right.Value);
Demo(data, left, partitionIndex - 1);
Demo(data, partitionIndex + 1, right);
}
return data;
}
//分块的 左边是啥??? 右边是啥??
static int partition(List<int> data, int left, int right)
{
int pivot = left, index = pivot + 1;
for (var i = index; i <= right; i++)
{
if (data[i] < data[pivot])
{
Swap(data, i, index);///交换i跟index
index++;
}
}
Swap(data, pivot, index - 1);///交换pivot与index-1
return index - 1;
}
static void Swap(List<int> data, int i, int j)
{
var temp = data[i];
data[i] = data[j];
data[j] = temp;
}
}
**三、时间复杂度分析 ** 快速排序的算法的执行时间取决于标准记录的选择。如果每次排序时所选取记录的关键字的值都是当前子序列的“中间数”,那么该记录的排序终止位置在该子序列的中间,这样就把原来的子序列分解成了两个长度基本相等的更小的子序列,在这种情况下,排序的速度最快。最好情况下快速排序的时间复杂度为O(nlog2n) 另一种极端的情况是每次选取的记录的关键字都是当前子序列的“最小数”,那第该记录的位置不变,它把原来的序列分解成一个空序列和一个长度为原来序列长度减1的子序列,这种情况下时间复杂度为O(n2)。因此若原始记录序列巳“正序”排列,且每次选取的记录都是序列中的第一个记录,即序列中关键字最小的记录,此时,快速排序就变成了“慢速排序”。 由此可见,快速排序时记录的选取是非常重要的。在一般情况下,序列中各记录的关键字的分布是随机的,所以每次选取当前序列中的第一个记录不会影响算法的执行时间,因此算法的平均比较次数为O(nlog2n)。 快速排序是一种不稳定的排序方法。

