用Go撸数据结构(三):链表
2020-06-05 14:36:53什么是链表
- 和数组一样,链表也是一种线性表。
- 从内存结构来看,链表的内存结构是不连续的内存空间,是将一组零散的内存块串联起来,从而进行数据存储的数据结构。
- 链表中的每一个内存块被称为节点Node。节点除了存储数据外,还需记录链上下一个节点的地址,即后继指针next。
链表的特点
- 插入、删除数据效率高O(1)级别(只需更改指针指向即可),随机访问效率低O(n)级别(需要从链头至链尾进行遍历)。
- 和数组相比,内存空间消耗更大,因为每个存储数据的节点都需要额外的空间存储后继指针。
常用链表
链表结构五花八门,本文来看一下最常见的三种链表结构,它们分别是:单链表、双向链表和循环链表。
链表通过指针将一组零散的内存块串联在一起。其中,我们把内存块称为链表的“结点”。为了将所有的结点串起来,每个链表的结点除了存储数据之外,还需要记录链上的下一个结点的地址。如图所示,我们把这个记录下个结点地址的指针叫作后继指针 next。
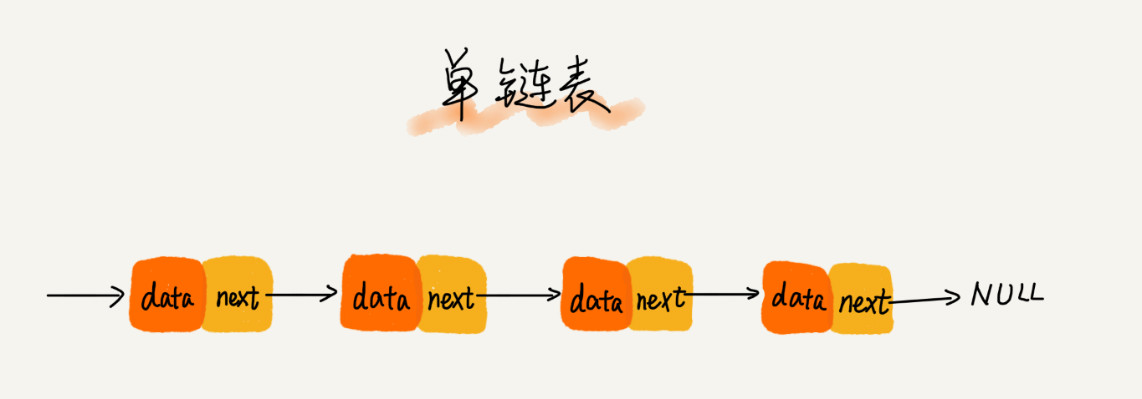
从图中可以发现,其中有两个结点是比较特殊的,它们分别是第一个结点和最后一个结点。我们习惯性地把第一个结点叫作头结点,把最后一个结点叫作尾结点。其中,头结点用来记录链表的基地址。有了它,我们就可以遍历得到整条链表。而尾结点特殊的地方是:指针不是指向下一个结点,而是指向一个空地址 NULL,表示这是链表上最后一个结点。
循环链表是一种特殊的单链表。实际上,循环链表也很简单。它跟单链表唯一的区别就在尾结点。我们知道,单链表的尾结点指针指向空地址,表示这就是最后的结点了。而循环链表的尾结点指针是指向链表的头结点。它像一个环一样首尾相连,所以叫作“循环”链表。
双向链表,顾名思义,它支持两个方向,每个结点不止有一个后继指针 next 指向后面的结点,还有一个前驱指针 prev 指向前面的结点。

从图中可以看出来,双向链表需要额外的两个空间来存储后继结点和前驱结点的地址。所以,如果存储同样多的数据,双向链表要比单链表占用更多的内存空间。虽然两个指针比较浪费存储空间,但可以支持双向遍历,这样也带来了双向链表操作的灵活性。
插入、删除操作比单链表效率更高O(1)级别。以删除操作为例,删除操作分为2种情况:给定数据值删除对应节点和给定节点地址删除节点。对于前一种情况,单链表和双向链表都需要从头到尾进行遍历从而找到对应节点进行删除,时间复杂度为O(n)。对于第二种情况,要进行删除操作必须找到前驱节点,单链表需要从头到尾进行遍历直到p->next = q,时间复杂度为O(n),而双向链表可以直接找到前驱节点,时间复杂度为O(1)。 对于一个有序链表,双向链表的按值查询效率要比单链表高一些。因为我们可以记录上次查找的位置p,每一次查询时,根据要查找的值与p的大小关系,决定是往前还是往后查找,所以平均只需要查找一半的数据。
如何基于链表实现 LRU 缓存淘汰算法
思路:我们维护一个有序单链表,越靠近链表尾部的结点是越早之前访问的。当有一个新的数据被访问时,我们从链表头开始顺序遍历链表。
- 如果此数据之前已经被缓存在链表中了,我们遍历得到这个数据对应的结点,并将其从原来的位置删除,然后再插入到链表的头部。
- 如果此数据没有在缓存链表中,又可以分为两种情况:
- 如果此时缓存未满,则将此结点直接插入到链表的头部;
- 如果此时缓存已满,则链表尾结点删除,将新的数据结点插入链表的头部。
现在我们来看下缓存访问的时间复杂度是多少。因为不管缓存有没有满,我们都需要遍历一遍链表,所以这种基于链表的实现思路,缓存访问的时间复杂度为 O(n)。
实际上,我们可以继续优化这个实现思路,比如引入散列表(Hash table)来记录每个数据的位置,将缓存访问的时间复杂度降到 O(1)。
写好链表的技巧?6大学习技巧
想要写好链表代码并不是容易的事儿,尤其是那些复杂的链表操作,比如链表反转、有序链表合并等,写的时候非常容易出错。要写好链表可以关注以下几个技巧:
一、理解指针或引用的含义
- 含义:将某个变量(对象)赋值给指针(引用),实际上就是就是将这个变量(对象)的地址赋值给指针(引用)。
- 示例: p—>next = q; 表示p节点的后继指针存储了q节点的内存地址。 p—>next = p—>next—>next; 表示p节点的后继指针存储了p节点的下下个节点的内存地址。
二、警惕指针丢失和内存泄漏
- 插入节点 在节点a和节点b之间插入节点x,b是a的下一节点,,p指针指向节点a,则造成指针丢失和内存泄漏的代码:p—>next = x;x—>next = p—>next; 显然这会导致x节点的后继指针指向自身。 正确的写法是2句代码交换顺序,即:x—>next = p—>next; p—>next = x;
- 删除节点 在节点a和节点b之间删除节点b,b是a的下一节点,p指针指向节点a:p—>next = p—>next—>next;
三、利用哨兵简化实现难度
- 什么是“哨兵”? 链表中的“哨兵”节点是解决边界问题的,不参与业务逻辑。如果我们引入“哨兵”节点,则不管链表是否为空,head指针都会指向这个“哨兵”节点。我们把这种有“哨兵”节点的链表称为带头链表,相反,没有“哨兵”节点的链表就称为不带头链表。
- 未引入“哨兵”的情况 如果在p节点后插入一个节点,只需2行代码即可搞定: new_node—>next = p—>next; p—>next = new_node; 但,若向空链表中插入一个节点,则代码如下: if(head == null) 如果要删除节点p的后继节点,只需1行代码即可搞定: p—>next = p—>next—>next; 但,若是删除链表的最有一个节点(链表中只剩下这个节点),则代码如下: if(head—>next == null) 从上面的情况可以看出,针对链表的插入、删除操作,需要对插入第一个节点和删除最后一个节点的情况进行特殊处理。这样代码就会显得很繁琐,所以引入“哨兵”节点来解决这个问题。
- 引入“哨兵”的情况 “哨兵”节点不存储数据,无论链表是否为空,head指针都会指向它,作为链表的头结点始终存在。这样,插入第一个节点和插入其他节点,删除最后一个节点和删除其他节点都可以统一为相同的代码实现逻辑了。
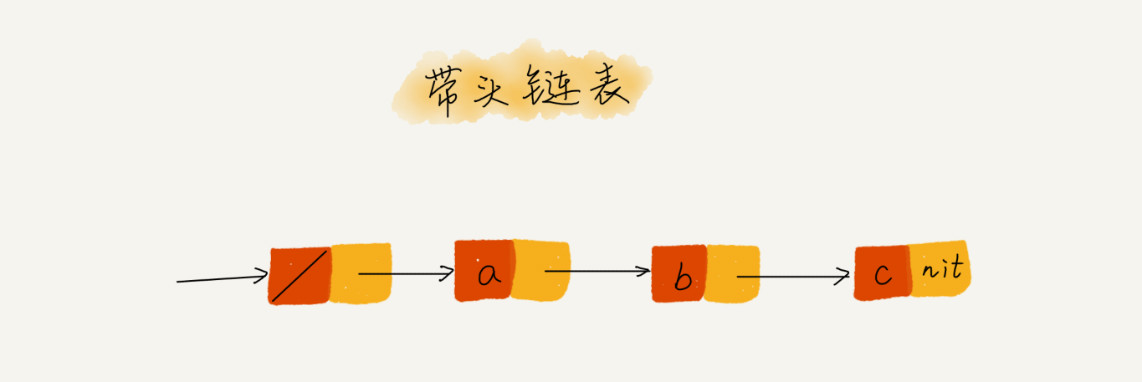
实际上,这种利用哨兵简化编程难度的技巧,在很多代码实现中都有用到,比如插入排序、归并排序、动态规划等。
四、重点留意边界条件处理
- 如果链表为空时,代码是否能正常工作?
- 如果链表只包含一个结点时,代码是否能正常工作?
- 如果链表只包含两个结点时,代码是否能正常工作?
- 代码逻辑在处理头结点和尾结点的时候,是否能正常工作?
五、举例画图,辅助思考
核心思想:释放脑容量,留更多的给逻辑思考,这样就会感觉到思路清晰很多。
六、多写多练,没有捷径
链表的常见问题
单链表反转
type ListNode struct {
data interface{}
Next *ListNode
}
func reverseList(head *ListNode) *ListNode {
cur := head
var pre *ListNode
for cur != nil {
cur.Next, pre, cur = pre, cur, cur.Next
}
return pre
}
链表中环的检测
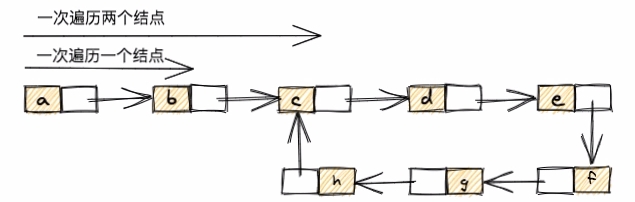
思路:最简单的方式,通过快慢指针的方式处理。有两个指针lowPtr和fastPtr,它们同时从头结点开始遍历链表中的所有结点。lowPtr为慢指针,一次遍历一个结点;fastPtr为快指针,一次遍历两个结点。如果链表中没有环,则fastPtr和lowPtr会先后遍历完所有的结点。如果链表中有环,则快慢指针会先后进入到环中,并且一定会在某一个结点相遇。如果相遇,则该链表中是有环的。
func checkRing(head *ListNode) bool {
low := head
fast := head
for fast.Next != nil {
low = low.Next
fast = fast.Next.Next
// 防止for中fast.Next出现nil
if fast == nil {
return false
}
if low == fast {
return true
}
}
return false
}
两个有序的链表合并
输入:3->6->9, 2->6->10 输出:2->3->6->6->9->10
func mergeTwoLists(l1 *ListNode, l2 *ListNode) *ListNode {
//如果有一条链是nil,直接返回另外一条链
if l1 == nil {
return l2
}
if l2 == nil {
return l1
}
// 定义一个结果节点
var result *ListNode
// 当l1节点的值大于l2节点的值,那么res指向l2的节点,从l2开始遍历,反之从l1开始
if l1.Val >= l2.Val {
result = l2
result.Next = mergeTwoLists(l1, l2.Next)
} else {
result = l1
result.Next = mergeTwoLists(l1.Next, l2)
}
return res
}
删除链表倒数第 n 个结点
func removeNthFromEnd(head *NodeList, n int) *NodeList {
if head == nil{
return nil
}
if n < 0 {
return head
}
i, j := head, head
z := 0
for ; i.Next != nil; i=i.Next{
if z < n+ 1 {
z++
continue
}
j = j.Next
}
if(z > n){
j.Next = j.Next.Next
}
return head;
}
求链表的中间结点
- 输入链表头节点,奇数长度返回中点,偶数长度返回上中点
func middleNode(head *ListNode) *ListNode {
pre := &ListNode{} //虚拟头节点
pre.Next = head
pre.Val = 1
slow := pre
fast := pre
for fast != nil && fast.Next != nil {
slow = slow.Next
fast = fast.Next.Next
}
return slow
}
- 输入链表头节点,奇数长度返回中点,偶数长度返回下中点 。
func middleNode(head *ListNode) *ListNode {
slow := head
fast := head
for fast != nil && fast.Next != nil {
slow = slow.Next
fast = fast.Next.Next
}
return slow
}

